Predicting Base Shear in Steel Frame Structures Using Hybrid Genetic Programming and Simulated Annealing

The assessment of base shear in steel frame structures subjected to seismic activity is a crucial element of structural engineering. Base shear is defined as the maximum lateral force exerted at the base of a structure during an earthquake. This phenomenon is influenced by various factors, including the number of bays and stories, soil type, structural bracing, natural period of the structure, site conditions, and seismic coefficients.

Traditional approaches, such as the Uniform Building Code (UBC) formula, offer empirical solutions; however, they often lack the precision required due to their generalized nature, failing to account for the intricate nonlinear interactions among these variables.

Recent advancements in artificial intelligence and computational optimization have led to the development of more reliable methods, such as the hybrid Genetic Programming and Simulated Annealing (GP/SA) technique. This discussion will explore how the GP/SA method surpasses conventional models in predicting base shear with enhanced accuracy and efficiency.

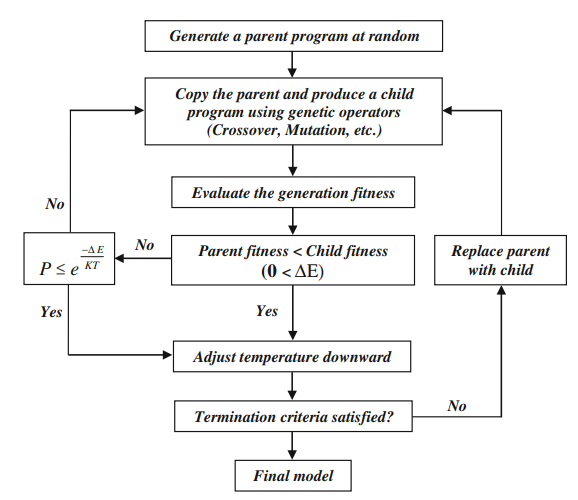
Genetic Programming (GP) applies principles of Darwinian natural selection to create computer models that solve problems. Unlike Genetic Algorithms (GAs), which represent solutions as sequences of numbers, GP models solutions as tree structures of computer programs, usually written in functional programming languages like LISP. In GP, programs evolve as parse trees of varying lengths, with optimization relying on a fitness landscape that evaluates each program’s capability to execute a specific task through a fitness function. The fundamental type of GP is tree-based GP, which generates a random population of hierarchically organized trees containing functions and terminals, chosen from predefined sets. Simulated Annealing (SA) mimics the annealing process, where metal is heated to a high temperature and then slowly cooled to relieve thermal stresses. As this occurs, each atom in the metal seeks a stable arrangement within the crystalline structure. The internal energy (E) of each state can be quantified and fluctuates with temperature changes. Generally, internal energy (ΔE) declines as temperature decreases, though occasional increases in energy may happen during cooling.

The study employs a hybrid of GA and SA, with SA selecting new individuals and LGP functioning as linear genetic programming. Unlike traditional GP, LGP replaces the functional programming language typically used (like LISP) with programs written in an imperative language (such as C/C++). The integrated GP/SA algorithm consists of several key steps to develop a computer program:

1.Generating an initial population of mathematical models using GP.

2.Evaluating fitness based on accuracy in predicting base shear.

3.Applying SA-based selection criteria to evolve the best models.

4.Fine-tuning equations to minimize errors and improve generalization.

The study incorporates four input features: the number of bays, the number of storeys, soil type, and the condition of being braced or unbraced for predicting base shear (V). It employed a FEA-based database to analyze plane steel structures, which are classified into I-type and II-type models based solely on their section properties. I-type models (Model A and B) feature specific beam and column sections designed for 1, 2, and 3 bay configurations, while II-type models (Model C and D) utilize a different selection of sections for their columns and beams. The models consist of unbraced frames (Model A and C) and braced frames (Model B and D), covering spans of 1–3 bays and buildings of 4–15 stories high. Furthermore, the analysis accounted for four soil classifications, leading to the examination of 192 distinct steel frames, with data represented through frequency histograms. Overall, the study used a dataset comprising 192 samples, which was divided into 80% for training and 20% for testing.

The GP/SA model was created using the database, employing the following parameters in the GP/SA algorithms:

• Number of temperature levels = [1000, 2000, 3000]
• Number of iterations per temperature level = 1500
• Start temperature = 5
• Stop temperature = 0.01
• Crossover rate (%) = 50, 95
• Homologous crossover (%) = 95
• Probability of randomly generated parent in crossover (%) = 99
• Block mutation rate (%) = 30
• Instruction mutation rate (%) = 30
• Data mutation rate (%) = 40
• Offspring choice rate (%) = 50
• Replacement scaling factor = 1
• Maximum program size = 128, 256
• Initial program size = 80
• Function set = +,-,x,/

The parameters mentioned herein were selected through a trial-and-error approach. The study employs four fundamental arithmetic operators to optimize the Genetic Programming/Simulated Annealing (GP/SA) model. To minimize error, each iteration was executed using a substantial number of temperature levels and iterations. The program continued until no significant reduction in error was detected across the runs.

The performance metrics of the GP/SA model were evaluated using several key indicators, including the Mean Absolute Error (MAE) and the Correlation Coefficient (R). In order to benchmark the performance of the GP/SA model, it was compared against traditional models, specifically the University of British Columbia (UBC) and Artificial Neural Network (ANN) models. The results indicated that the GP/SA model demonstrated superior performance compared to these traditional methods, showcasing enhanced predictive capabilities. In this comparison, the GP/SA model attained a correlation coefficient of 0.965 and a mean absolute error of 12,272, establishing it as the most accurate model for base shear predictions. This result surpassed that of the UBC model, which yielded a correlation coefficient of 0.947 and a MAE of 15,936, and also outperformed the ANN model, which produced a correlation of 0.879 with a MAE of 12,762. Moreover, the classical Genetic Programming (GP) model, which exhibited a correlation of 0.958 and a MAE of 12,986, was similarly outperformed by the GP/SA model, further reinforcing its efficacy and reliability in predictive applications.

A sensitivity analysis was conducted to evaluate the influence of various input parameters on base shear. The number of stories (N_s) in a structure is of considerable significance, as taller buildings are subjected to increased base shear owing to amplified lateral forces. Similarly, the number of bays (N_b) contributes to greater flexibility, which in turn affects the distribution of shear across the structure. Furthermore, the type of soil (Z) plays a pivotal role in influencing base shear; softer soils generally result in elevated shear levels due to increased seismic amplification. The bracing condition (B) is another crucial factor, as braced structures typically demonstrate lower shear values due to improved stability. These observed phenomena are consistent with fundamental engineering principles, thereby providing further validation for the GP/SA model.

The integration of Genetic Programming and Simulated Annealing presents a robust methodology for the prediction of base shear in steel frame structures. By utilizing AI-driven optimization techniques, the GP/SA model achieves enhanced accuracy compared to conventional methods, establishing it as an invaluable resource for seismic design and structural evaluation. As computational techniques continue to advance, hybrid models such as GP/SA are expected to assume an increasingly essential role in engineering applications.