Delhi Technical University Researchers Develop SVM Model for Accurate Water Surface Profile Prediction

Predicting water surface profiles in rivers and channels is essential for flood management and hydraulic design. With a growing global population near rivers, flooding poses significant threats to life and economy. Accurate prediction of river flow rates is vital for flood prevention, leading to interest in assessing discharge, velocity, shear stress, and water levels. Compound channels often form during overbank flows, affecting floodplain morphology and creating two-stage channels. Energy transfer between main channels and flood zones is critical in composite waterways, complicating flow replication. While previous research has focused on straight and meandering channels, non-prismatic compound channels are less understood. Variations in channel shapes influence flow and momentum transfer, with studies indicating that asymmetrical geometry boosts mass transfers and head losses. In curved channels, expanding floodplains can increase velocity gradients and head losses due to momentum transfer. Past research shows changes in depth and roughness ratios influence velocity gradients and shear stress.

There are several methods for predicting water surface profiles, but they present challenges primarily due to their dependence on intricate mathematical models. Traditional hydrodynamic techniques employ complex equations, like the Saint-Venant equations, which focus on the principles of mass and momentum conservation, along with Manning’s equation, used for estimating flow velocity based on channel roughness. While finite element models are also used, they often demand significant computational resources. Although these methods can provide accurate results, they require high-quality data and substantial computation time.

In this context, machine learning emerges as a promising alternative, potentially optimizing the prediction process and enhancing efficiency. Several machine learning techniques have been explored in previous studies, including support vector machine (SVM), genetic expression programming (GEP), and artificial neural networks (ANN). Notably, GEP reveals unique mathematical relationships frequently overlooked in river engineering. Research indicates that SVM achieves high accuracy in discharge predictions through various analytical methods such as single channel method (SCM), coherence method (COHM), and divided channel method (DCM). The multilayer perceptron (MLP) and multivariate adaptive regression splines (MARS) model demonstrate superior performance with greater accuracy. Importantly, GEP results closely match empirical data, suggesting that the estimated proportion of shear force supported by floodplains aligns well with observed figures, thereby assisting in determining the boundary shear force influenced by floodplains.

Predicting water surface profiles is critically important for designing safe and efficient water management systems. This need is especially pronounced in non-prismatic compound channels, which feature varying widths and slopes, as turbulent flow dynamics make water level predictions much more complicated. Accurate predictions of water surface elevation are vital for several reasons: they aid in flood prevention and control, guide the design of essential infrastructure like bridges, dams, and embankments, and support river restoration projects and sediment transport studies. A solid grasp of these dynamics empowers engineers to devise effective strategies for managing water resources and minimizing potential hazards.

With the rise of machine learning models, powerful alternatives have emerged for predicting water surface profiles accurately and efficiently. This article examines a study by Vijay Kaushik and Munendra Kumar from the Department of Civil Engineering at Delhi Technological University, Delhi, India, focused on predicting water surface profiles in non-prismatic compound channels using support vector machines (SVM). The article discusses how SVM has the potential to revolutionize hydraulic engineering and enhance flood risk assessment. 

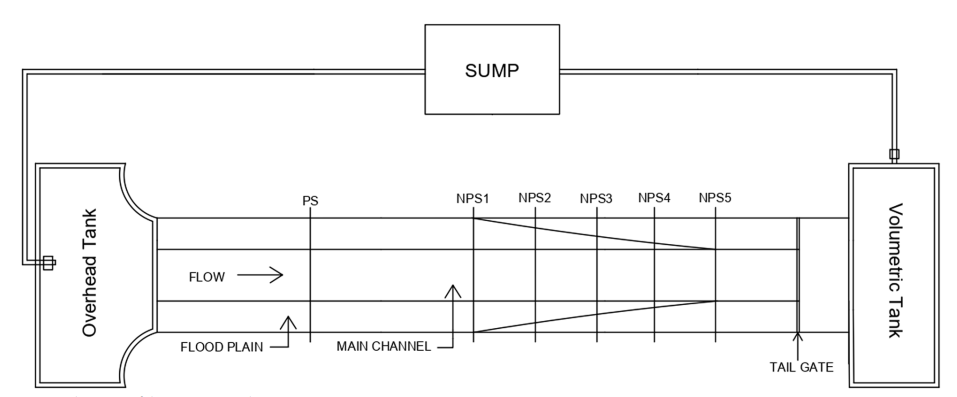
The authors established a small-scale setup in a hydraulic lab and carried out experiments. The setup was structured as follows:

Experiment setup included a masonry flume:

• Length: 12 m
• Width: 1 m
• Depth: 0.8 m
• Main channel width: 0.5 m
• Main channel depth: 0.25 m

Flume features:

• Converging angle: 4°
• Non-prismatic geometry
• Converging length: 3.6 m
• Subcritical flow measurements taken under various conditions with a longitudinal bed slope of 0.001.
• Manning’s n value determined from data collected during in-bank and over-bank flows.
• Water recycling system in place, pumping from an underground sump to a reservoir:
• Flow collected in a volumetric receptacle before returning to the sump.

The authors employed an Acoustic Doppler Velocimeter (ADV) to assess the three-dimensional velocity distribution, while the lateral distributions of boundary shear stress were measured using a 5 mm outer diameter Preston tube at the same sections where the velocity distributions were analyzed. A digital manometer was used to gauge the pressure difference. Calibration equations developed by V.C. Patel from Cambridge University were then applied to calculate the shear stress values. Measurements of local boundary shear stress and velocity were taken along the wetted perimeter at intervals of 2.5 cm vertically and 10 cm horizontally.

Support Vector Regression (SVR) is a machine learning algorithm designed for regression analysis. It operates on principles akin to support vector machines (SVMs) but focuses on predicting continuous output variables. The core concept of SVR is identifying a function that maps input variables to output variables while minimizing errors and adhering to a defined margin. To accomplish this, it transforms input variables into a higher-dimensional space through a kernel function. SVR effectively addresses non-linear relationships among variables by employing kernel functions such as polynomial, radial basis function (RBF), and sigmoid to capture intricate associations. The authors created a dataset considering factors like width ratio (α), relative depth ratio (β), aspect ratio (δ), converging angle (θ), relative distance (Xr), and longitudinal bed slope (So) to assess the water surface profile of composite waterways with convergent floodplains. The dataset was split into 70% for training and 30% for testing, and the analysis was carried out in the MATLAB environment. The optimal hyperparameters for SVM were determined through trial and error. Furthermore, the kernel functions used (linear, RBF, polynomial, and sigmoid) help reduce the input space’s dimensionality, easing the classification process.

The flow behaviour of water in a non-prismatic composite channel has several unique features. In the straight sections, the water level stays steady; however, in the converging areas, the flow velocity rises while the water level falls. As the flow depth increases, the width ratio leads to a broader water surface profile, with consistent changes corresponding to this ratio. It’s crucial to understand that the increase in the water surface does not have a linear relationship with the interaction depths of the two flows. Moreover, the aspect ratio of the water surface profile decreases as it moves through different parts of the channel. The impact of distance on the water surface representation lessens as the separation between points increases, and sharper convergence angles in floodplains significantly reduce potential head. The SVM model shows remarkable predictive accuracy, with an R² value of 0.99 and an RMSE of 0.0199. Furthermore, it achieves a mean absolute percentage error (MAPE) of 1.263, making it the most effective method for predicting water surface profiles in compound channels with narrowing floodplains.

Using Support Vector Machine (SVM) for predicting water surface profiles represents a notable improvement in hydraulic modeling. SVM offers high accuracy, lower computational costs, and the ability to adapt to non-linear situations, making it a viable alternative to conventional hydraulic models. As AI technology advances, incorporating it into water resource management will improve flood forecasting, infrastructure development, and environmental protection.